 |
Das deutsche QBasic- und FreeBASIC-Forum
Für euch erreichbar unter qb-forum.de, fb-forum.de und freebasic-forum.de!
|
| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 07.06.2014, 16:51 Titel: Graph ausmessen ... Verfasst am: 07.06.2014, 16:51 Titel: Graph ausmessen ... |
 |
|
zugegeben der fred ist etwa magic-topíc. Vielleicht aber auch nicht so sehr.
Gibt es ein QB-Programm mit dessen Hilfe die Fläche unter einem Graphen vermessen werden kann?
Wahrscheinlich kann man mit QB einen Graphen nicht einfach einscannen und dann bearbeiten? Oder täusche ich mich da?
Aber doch eher so: Ich stelle mir das so vor, dass man einzelne Punkte des Graphen eingibt und das QBprogramm den Rest der Rechnung erledigt.
Ist Euch ein solches Programm bekannt?
grüsse nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 07.06.2014, 17:44 Titel: Verfasst am: 07.06.2014, 17:44 Titel: |
 |
|
Du kannst einen auf dem Bildschirm befindlichen Graphen natürlich schon "einscannen" - spaltenweise von der obersten Zeile so lange nach unten, bis POINT den Farbwert deines Graphen zurückgibt. Und von diesem aus dann den Abstand zur x-Achse bestimmen und aufaddieren.
Vielleicht habe ich heute abend ja noch Lust, schnell was zu schreiben, wir haben nur leider gerade so schönes Wetter  - aber es sollte auf jeden Fall klar sein, dass die Berechnung über den Graphen ziemlich ungenau werden wird. Über den Funktionsterm ist es dann schon besser, aber auch immer nur eine Näherung. - aber es sollte auf jeden Fall klar sein, dass die Berechnung über den Graphen ziemlich ungenau werden wird. Über den Funktionsterm ist es dann schon besser, aber auch immer nur eine Näherung.
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 07.06.2014, 17:49 Titel: Verfasst am: 07.06.2014, 17:49 Titel: |
 |
|
Hi nemored:
Danke, dass Du Dich in der Sache meldest.
Es wäre wirklich schön, wenn Du mal ein kleines Testskribt hinbekämst.
Soweit mal schöne Pfingsten
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 07.06.2014, 21:27 Titel: Verfasst am: 07.06.2014, 21:27 Titel: |
 |
|
Ich programmiere schon seit über zehn Jahren nicht mehr mit QBasic, daher kann ich nicht garantieren, dass alles einwandfrei läuft - aber ich denke, wenn Anpassungen nötig sein sollten, dürften die nur minimal sein.
Die Methode durch Auslesen aus der Zeichnung funtioniert natürlich nur, wenn der ganze Graph auf den Bildschirm passt. Der exakte Flächeninhalt unter dem Kosinusbogen wäre 2.
| Code: | screen 12
function f(x as double) as double
f = cos(x)
end function
dim x as double
dim y as double
dim start as double
dim ende as double
dim schritt as double
dim faktorX as integer
dim faktorY as integer
dim summe1 as double
dim summe2 as double
start = -1.570796327
ende = 1.570796327
faktorX = 100
faktorY = 100
schritt = .01
line (0, 240)-(639, 240), 2
line (320, 0)-(320, 479), 2
for x = start to ende step schritt
y = f(x)
pset (320 + x*faktorX, 240 - y*faktorY)
' aufaddieren (Streifenmethode)
summe1 = summe1 + y*schritt
next
' Graph 'scannen' und Flächeninhalt aufsummieren
for x = start to ende step schritt
for y = 0 to 639
if point (320 + x*faktorX, y) = 15 then
' aufaddieren
summe2 = summe2 + (240-y)/faktorY*schritt
exit for
end if
next
next
print "Direktberechnung: "; summe1
print "vom Graphen abgelesen: "; summe2
sleep |
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 13.06.2014, 17:12 Titel: Verfasst am: 13.06.2014, 17:12 Titel: |
 |
|
Hi nemored:
Dank für Deine Mühe. Bin erst jetzt wieder online.
Hast Du denn das Teil mal ausprobiert? Ich muß den Code erst mal laufen lassen; das dauert eine Weile. Und dann muß ich versuchen den zu verstehen.
Ein paar Fragen hätte ich schon jetzt:
-Das Teil zähl Pixel, hab ' ich das richtig verstanden?
-Die y-Werte sind begrenzt durch die Kosinusfunktion?
-Was sind das für Zahlen bei den Variablen start und ende?
(Mit was programmierst Du heutzutage?)
Ich melde mich wieder.
Grüsse Nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
Sebastian
Administrator

Anmeldungsdatum: 10.09.2004
Beiträge: 5969
Wohnort: Deutschland
|
 Verfasst am: 13.06.2014, 18:47 Titel: Verfasst am: 13.06.2014, 18:47 Titel: |
 |
|
| nemored hat Folgendes geschrieben: | | Ich programmiere schon seit über zehn Jahren nicht mehr mit QBasic |
| Nils hat Folgendes geschrieben: | | (Mit was programmierst Du heutzutage?) |
Ich komme nemored mal beim Antworten zuvor: Unter anderem mit FreeBASIC. Das ist der inoffizielle Open-Source-Nachfolger von QBasic. Behebt die Schwächen von QB (das Jahrzehnte alte 16-Bit-DOS-Software ist) und erweitert das ganze um alle modernen Funktionen und Annehmlichkeiten, die heute normal sind. FreeBASIC erzeugt native Anwendungen u. a. für Windows und Linux, jeweils 32- und 64-bittig.
nemored hat zum Beispiel dieses E-Book hier geschrieben:
http://www.freebasic-portal.de/projekte/openbook-2d-spieleprogrammierung-59.html
Zum eigentlichen Thema:
| Nils hat Folgendes geschrieben: | | Aber doch eher so: Ich stelle mir das so vor, dass man einzelne Punkte des Graphen eingibt und das QBprogramm den Rest der Rechnung erledigt. |
Wenn man das mathematisch richtig lösen will (statt durch Abzählen von Pixeln auf einem Grafik-SCREEN), müsste man ungefähr wie folgt vorgehen:
- Aus den gegebenen Punkten ein Polynom aufstellen, auf dessen Graph alle Punkte liegen => f(x)
- Stammfunktion (-> unbestimmtes Integral) von f(x) bilden => F(x)
- Untere und obere Grenze auf der x-Achse festlegen (Von wo bis wo soll die Fläche unter dem Graphen bestimmt werden?)
- Bestimmtes Integral von unterer bis oberer Grenze berechnen => Orientierter Flächeninhalt
Um sowas exakt / rechnerisch zu lösen, braucht man ein Computer-Algebra-System oder eine Sprache, die auf mathematische Aufgabenstellungen hin optimiert ist. Die meisten Programmiersprachen bzw. ihre Standardbibliotheken beinhalten von Haus aus keine Funktionen zum Umformen / Auflösen von Gleichungen / Gleichungssystemen, zum Differenzieren oder Integrieren.
Wenn man es grafisch durch das Auszählen von Pixeln in QB löst, ist das immer nur ein Näherungswert.
_________________

Die gefährlichsten Familienclans | Opas Leistung muss sich wieder lohnen - für 6 bis 10 Generationen! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 13.06.2014, 19:00 Titel: Verfasst am: 13.06.2014, 19:00 Titel: |
 |
|
| Nils hat Folgendes geschrieben: | -Das Teil zähl Pixel, hab ' ich das richtig verstanden?
-Die y-Werte sind begrenzt durch die Kosinusfunktion? |
Richtig; das Programm zählt von oben nach unten durch, ob es einen Graphenpunkt findet; wenn ja, dann bestimmt es den Abstand zur x-Achse.
| Zitat: | | -Was sind das für Zahlen bei den Variablen start und ende? |
Der Start- und Endwert meiner Funktion (x-Werte), in diesem Fall - PI / 2 bis + PI / 2
Und ja, selbstverständlich habe ich das Programm getestet  aber eben nicht in QBasic, (das ich gar nicht mehr besitze) sondern in FreeBASIC. Vom Prinzip her müsste es also auch in QBasic funktionieren. aber eben nicht in QBasic, (das ich gar nicht mehr besitze) sondern in FreeBASIC. Vom Prinzip her müsste es also auch in QBasic funktionieren.
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 14.06.2014, 16:50 Titel: Verfasst am: 14.06.2014, 16:50 Titel: |
 |
|
@ Sebastian:
Free basic? Muß ich auch ausprobieren! Bei Gelegenheit! Hoffe nur das Umlernen ist nicht so schwer.
Zur Sache: Was Du meinst ist eine numerische Intergration, Fass-Regel u.ähnl. was ich ja gerade nicht meine. Mir ngeht es wirklich ums Auszählen.
@ nemored:
Hab' das prog gerade man laufen lassen(wollen)! Schon werden Fehler angemeckert. Leider habe ich eine italienische Version ohne Hilfsfunktion, so dass ich reichlich auf dem Schlauch stehe.
Gemeckert wurde schon in Zeile 2 und das zweite as unterlegt.
Danach in Z 5, wenn ich das richtig deute: weil die Variable bereits definiert sei.
Was ich mit den Grenzen meinte, ging eher in die Richtung Normierung. Eine bestimmte Anzahl Pixel sagt ja für sich allein kaum etwas. Hat man aber normiert, kann man die Pixel einer Maßzahl zuordnen und erhält eine aussagekräftige Berechnung.
FreeBasic. Ist das eine gute Wahl? Ich schreibe eigentlich nur Alogorithmen und beschränke mich auf eine Ausgabe der Daten in ein File. Wenn ich umlernen soll, dann sollten da erhebliche Vorteile dafürt sprechen. Kann man mit FB exe Dateien erstellen? Kann ich einfache Oberflächengestaltung machen? Iwstr das Teil wesentlich schneller als QB? Das wären meine Fragen dazu.
Tolles Spiel gestern abend! Wat?
grüsse nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
Elor
Anmeldungsdatum: 12.07.2013
Beiträge: 205
Wohnort: Konstanz
|
 Verfasst am: 14.06.2014, 18:15 Titel: Verfasst am: 14.06.2014, 18:15 Titel: |
 |
|
| Zitat: |
Hab' das prog gerade man laufen lassen(wollen)! Schon werden Fehler angemeckert. Leider habe ich eine italienische Version ohne Hilfsfunktion, so dass ich reichlich auf dem Schlauch stehe.
|
Warum Laedst du dir nicht einfach ne Deutsche Version runter? Auf www.qbasic.de, unter Downloads-Compiler kannst du dir QBASIC 1.1 (Interpreter-Deutsch) holen oder QuickBasic 4.5(Compiler-Deutsch) bzw QuickBasic 7.1(Compiler-Englisch). Dann kannst auch was mit den Fehlermeldungen anfangen. |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 14.06.2014, 19:46 Titel: Verfasst am: 14.06.2014, 19:46 Titel: |
 |
|
Um mal direkt auf die Fragen einzugehen:
| Zitat: | | FreeBasic. Ist das eine gute Wahl? |
Ja, auf jeden Fall. 
| Zitat: | | Ich schreibe eigentlich nur Alogorithmen und beschränke mich auf eine Ausgabe der Daten in ein File. Wenn ich umlernen soll, dann sollten da erhebliche Vorteile dafürt sprechen. |
Ein Vorteil bei FB ist, dass es nicht übermäßig viel umzulernen gibt. Im Portal gibt es eine Zusammenstellung, aber mal so in Kürze: Jede Variable muss explizit mit Typenangabe deklariert werden, es gibt keine Variablen-Suffixe mehr; wenn du das berücksichtigst, hast du schon über 90% des Umstiegs geschafft.
Sonst zum Nachlesen: http://www.freebasic-portal.de/befehlsreferenz/fb-dialektformen-459.html im Abschnitt "-lang fb"
| Zitat: | | Kann man mit FB exe Dateien erstellen? [...] Iwstr das Teil wesentlich schneller als QB? |
FB ist ein Compiler, d. h. du bekommst dein Programm ausschließlich dadurch zum Laufen, dass du aus ihm eine exe-Datei erstellst. QB ist ja zunächst einmal ein Interpreter.
In FB sehen die Arbeitsschritte so aus: Quelltext tippen, speichern, compilieren (-> exe-Datei), Programm ausführen. Eine gute IDE nimmt dir die einzelnen Punkte in der Regel ab, sodass du über eine einzige Taste das Programm speichern, compilieren und ausführen kannst, um es zu testen.
Bedingt dadurch, dass du nun ein compiliertes Programm vorliegen hast, läuft das natürlich auch wesentlich schneller als ein QB-Programm im Interpreter.
| Zitat: | | Kann ich einfache Oberflächengestaltung machen? |
Du kannst in FB jede C-Bibliothek verwenden (sofern die Header dazu vorliegen), einschließlich WinAPI und GUIs wie GTK, Qt oder wx-c. Der FreeBASIC-Editor wxFBE z. B. hat einen Designer für wx-c-Oberflächen mit dabei.
http://www.freebasic-portal.de/projekte/wxfbe-69.html
| Zitat: | | Was ich mit den Grenzen meinte, ging eher in die Richtung Normierung. Eine bestimmte Anzahl Pixel sagt ja für sich allein kaum etwas. Hat man aber normiert, kann man die Pixel einer Maßzahl zuordnen und erhält eine aussagekräftige Berechnung. |
Ich weiß jetzt nicht ganz genau, worauf du hinaus willst. Die Darstellung des Pixels auf dem Bildschirm entspringt ja ebenfalls einer Normierung (1 LE entspricht x Pixel; was im Übrigen im Quelltext über den Streckungsfaktor einstellbar ist). Das grundsätzliche Problem ist, dass eine Ansammlung von Pixeln bzw. Messdaten immer eine diskrete Menge ist, der Graph der zugehörigen Funktion dagegen unendlich viele Zwischenwerte besitzt.
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 16.06.2014, 09:45 Titel: Verfasst am: 16.06.2014, 09:45 Titel: |
 |
|
Hi nemored:
Hintergrund der Frage nach dem Erstellen von exes war, dass ich auch über eine qb-Version verfüge, mit der man das tun kann[Ist nur nix zur Hand zZ].
| Zitat: | | Du kannst in FB jede C-Bibliothek verwenden (sofern die Header dazu vorliegen), einschließlich WinAPI und GUIs wie GTK, Qt oder wx-c. Der FreeBASIC-Editor wxFBE z. B. hat einen Designer für wx-c-Oberflächen mit dabei. |
Ja, da bin ich schon nicht mehr zuhause. Sollte mich aber mal darum kümmern; bräuchte nur einen guten Lernpfad. Den Du vielleicht bereits in Deinem letzten post emphohlen hast?
Mit dem Normieren meine ich die Zuordnung zB einer Flächeneinheit zu einem Pixel. Ich will ja die Fläche unter einem Graphen, der als Funktion nicht vorhanden ist. Es gibt(anders als in Deinem Beispiel) nur die Kurve. Wenn ich aber jetzt zB einen Meßpunkt an irgendeiner x-Stelle habe, kann ich ggfls. die -ich sag' mal "Auswirkung"- der Gesamt-Fläche unter dem Graphen dem Meßwert zuordnen. Mich interessieren aber die mehr oder minder breiten Streifen unter der Kurve, nicht nur die Gesamtfläche. Wenn ich nun die Gesamtwirkung durch die Gesamtpixel teile, dann habe ich auf Teilwirkung pro Pixel normiert. Dann wird es nutzbringend.
Wenn Du also von -pi/2 bis +pi/2 eine Fläche unter Deinem Graphen auspixelst und in obige Beziehung zur eingeschlossenen Fläche setzt erhältst Du die Kurvenfläche pro Pixel. Jetzt kannst Du damit beliebig arbeiten.
Das erscheint im Beispiel zwar jetzt nicht sehr sinnvoll, weil Du die Normierung nur duchführen kannst, wenn Du die Fläche schon kennst, was ohne Meßwert nur geht, wenn Du die Funktion von -pi/2 bis +pi/2 integrierst.
Bitte poste doch mal Deine Ergebisse[Integration + gezählte Pixel].
Zusatzfrage: Die Genauigkeit ist ja durch die Größe eines Pixels begrenzt. Kann man denn die Kurve irgendwie "strecken", dann zählen und danach natürlich das Ergebnis wieder auf die ursprüngliche Kurve reduzieren? Das Ergebnisswürde genauer sein, da sich die Pixelquadrate besser an die Kurve anpassen würden.
Was meinst Du?
Du definierst ja ein Signal sobald der Graph ein Pixel berührt[bzw. identisch damit ist]. Da endet bzw. beginnt deine Zählung. Könntest Du mal versuchen das zu variieren?
Ich meine so: Einmal zählst Du alle Pixel einer Spalte ohne das Pixel, das den Graphen berührt. Bei der Alternativen alle inkl. des Pixels über dem Graphen, das den Graphen nicht mehr berührt. [Wird denn durch ein einziges Pixel ein einziger Graphenpunkt dargestellt?]
Die Flächen werden natürlich unterschiedlich groß. Aber das Mittel der beiden Flächen ist interessant. Entspricht das Deinem jetzigen Ergebnis?
grüsse nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 16.06.2014, 15:42 Titel: Verfasst am: 16.06.2014, 15:42 Titel: |
 |
|
(Ich hoffe immer noch, dass wir nicht aneinander vorbei reden.  ) )
Der Graph entsteht ja durch die Zeichnung der vorhandenen Messwerte; dass ich hier die Kosinuskurve genummen habe und nicht z. B. Zufallswerte, liegt nur daran, dass man das Ergebnis leichter überprüfen kann. Der berechnete Flächeninhalt war zumindest auf zwei Nachkommastellen genau (weiß jetzt das Ergebnis nicht auswendig).
Wenn dir die einzelnen Messdaten vorliegen und nicht in erster Linie der Graph, dann ist ein vorheriges Zeichnen des Graphen sowieso eher unsinnig. Der Graph dient ja nur dazu, die Messdaten wieder in den Computer zu bekommen. Die "exakte" Methode wäre, wie von Sebastian beschrieben, eine Interploation der Funktion und anschließender Integration; dazu brauchst du allerdings ein Computeralgebrasystem. Als Näherungswert würde ich das anders machen:
Messdaten nach Größe (x-Werte) sortieren und immer näherungsweise den Flächeninhalt zwischen zwei Messpunkten ermitteln. Hier kannst du ganz gut Trapeze verwenden. Wenn die Messwerte (x1 / y1) und (x2 / y2) lauten, dann ist der dazugehörige Flächeninhalt
A = (y1 + y2) / 2 * (x2 - x1)
Damit bist du unabhängig davon, wie "dicht" deine Messwerte beieinander liegen und ob sie äquidistant sind oder nicht. Bei n Messwerten bekommst du dann (n-1) Flächenstücke, die du aufaddierst. So weit die Theorie; ich hoffe, es hat sich kein Denkfehler eingeschlichen.
| Zitat: | Zusatzfrage: Die Genauigkeit ist ja durch die Größe eines Pixels begrenzt. Kann man denn die Kurve irgendwie "strecken", dann zählen und danach natürlich das Ergebnis wieder auf die ursprüngliche Kurve reduzieren? Das Ergebnisswürde genauer sein, da sich die Pixelquadrate besser an die Kurve anpassen würden.
Was meinst Du? |
In meinem Beispiel kannst du die Kurve über faktorX und faktorY beliebig strecken (macht natürlich nur Sinn, solange sich die Graphenpunkte noch alle auf dem Bildschirm befinden). Wenn der Graph auf einzelnen Messdaten beruht, wird das Strecken nicht mehr sinnvoll sein; du streckst ja nur die Bereiche, in denen gar keine Zwischenwerte vorliegen.
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
grindstone
Anmeldungsdatum: 03.10.2010
Beiträge: 1293
Wohnort: Ruhrpott
|
 Verfasst am: 17.06.2014, 08:18 Titel: Verfasst am: 17.06.2014, 08:18 Titel: |
 |
|
Hallo Nils!
Du sprichst in deinem letzten Posting von "Messpunkten". Hast du die Absicht, den Effektivwert (RMS) einer Messkurve zu ermitteln? Der wird nämlich (etwas) anders berechnet als durch einfaches Integrieren.
Gruß
grindstone
_________________
For ein halbes Jahr wuste ich nich mahl wie man Proggramira schreibt. Jetzt bin ich einen! |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 17.06.2014, 14:02 Titel: Verfasst am: 17.06.2014, 14:02 Titel: |
 |
|
@grindstone
Effektivwert? RMS?
Interessant! Bitte erklär' doch mal!
grüsse Nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 17.06.2014, 14:40 Titel: Verfasst am: 17.06.2014, 14:40 Titel: |
 |
|
RMS (Root Mean Square) ist das quadratische Mittel; hier werden die Quadrate aufaddiert und vom (arithmetischen) Mittelwert der Quadrate die Quadratwurzel gezogen. "Ausreißer-Werte" werden dabei stärker berücksichtigt als beim arithmetischen Mittel. Beim Effektivwert läuft das wieder über Integration, aber eben ein bisschen anders.
http://de.wikipedia.org/wiki/Effektivwert
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 17.06.2014, 16:44 Titel: Verfasst am: 17.06.2014, 16:44 Titel: |
 |
|
@nemored:
Hi! Wieder da? Oder bist Du unter mehreren Handles unterwegs?
Bitte poste doch mal Deine Ergebnisse. Ich meine die gezählten Pixel. 2/Pixelgesamtzahl sind dann ja Fläche pro Pixel. Wenn Du dann eine andere Funktion wählst, deren Fläche auf einem Intervall Du kennst, dann könnte man damit eine Nagelprobe vornehmen.
grüsse Nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 17.06.2014, 17:07 Titel: Verfasst am: 17.06.2014, 17:07 Titel: |
 |
|
| Nils hat Folgendes geschrieben: | | Hi! Wieder da? |
Wieso? War ich denn weg? oO
Zum Flächeninhalt:
Direktberechnung mit den berechneten "Masswerten": 1.9999900283007918
Erst zeichnen, dann wieder aus dem Graphen auslesen und mit diesem Wert weiterrechnen: 2.000500000000001
Korrekter Wert (Integration): 2
Andere Funktion: f(x) = 4 - x^2
Damit es ins Fenster passt: faktorX = 100, faktorY = 40
start = -2, ende = 2 (Nullstellen)
Direktberechnung: 10.6666
Über die Graphenpunkte: 10.6645
Korrekter Wert (Integration): 10 2/3
f(x) = exp(x); faktorX = 100, faktorY = 50, start = 0, ende = 1
Direktberechnung: 1.709704738308123
Über die Graphenpunkte: 1.7106
Exakter Wert (Integration) = e - 1, ist ungefähr 1.718281828
Hier ist der Wert über das Zeichnen und wieder Auslesen lustigerweise genauer. Wenn ich ein anderes faktorY wähle, sieht es schon wieder anders aus.
Was magst du noch?
Ach ja, nochmal zur Verdeutlichung: Ich zähle nicht die Pixel, sondern ich berechne, welchen Abstand das Pixel zur x-Achse hat und addiere diese Abstände.
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
Nils
Anmeldungsdatum: 24.03.2006
Beiträge: 191
|
 Verfasst am: 17.06.2014, 18:23 Titel: Verfasst am: 17.06.2014, 18:23 Titel: |
 |
|
Hi!
Das sieht ja sehr gut aus, Deine Berechnungsergebnisse!
Aber irgendetwas kommt mir da noch spanisch vor!
Der Abstand eines Punktes von der Abszisse ist doch nur dann ein Maß für die Fläche, wenn er ein solches darstellt. Du mußt also einen Streifen berechnen, den Du aber gar nicht hast. Denn ein delta x habe ich nicht vorgegeben. Du nimmst also irgendwo eine Streifenbreite her; d.h. Du integrierst im engen Sinne des Wortes.
Meine Idee war, die Fläche dadurch zu erhalten, dass ich die kleinsten Flächeneinheiten -die Pixel- zähle. Das sind sozusagen die kleinsten Quadrate auf dem Millimeterpapier. Und da wir nicht wissen wie groß die Fläche eines Pixels ist, werden alle gezählt und mit einem Ergebniss, das aufgrund eines Messpunktes errechnet werden kann verglichen. Es ergibt sich das Maß eines Pixels. Eigentlich war es da, was mir vorschwebte: Dumpf Kleinstflächen von der Nulllinie bis zum Graphen zählen. Das kann ja der Rechner besser als wir.
Wahrscheinlich kommt es im rechner nicht zum Pixelkonflikt: Der Graph wird dadurch gekennzeichnet sein, dass unmittelbar ober- und unterhalb des Graphenpixels Normalpixel sind. Oder?
grüsse nils
_________________
Kontrolliert die Politik! Laßt nicht die Politik Euch kontrollieren! Das sind Eure Angestellten! Lasst Sie das spüren!!! |
|
| Nach oben |
|
 |
Sebastian
Administrator

Anmeldungsdatum: 10.09.2004
Beiträge: 5969
Wohnort: Deutschland
|
 Verfasst am: 17.06.2014, 19:25 Titel: Verfasst am: 17.06.2014, 19:25 Titel: |
 |
|
| Nils hat Folgendes geschrieben: | Der Abstand eines Punktes von der Abszisse ist doch nur dann ein Maß für die Fläche, wenn er ein solches darstellt. Du mußt also einen Streifen berechnen, den Du aber gar nicht hast. Denn ein delta x habe ich nicht vorgegeben. Du nimmst also irgendwo eine Streifenbreite her; d.h. Du integrierst im engen Sinne des Wortes.
Meine Idee war, die Fläche dadurch zu erhalten, dass ich die kleinsten Flächeneinheiten -die Pixel- zähle. Das sind sozusagen die kleinsten Quadrate auf dem Millimeterpapier. |
Der Grafik-Screen beginnt sowohl in QBASIC als auch in FreeBASIC oben links im Ursprung (0,0). Zum Beispiel im SCREEN 12 wäre die Ecke ganz unten rechts (639,479), sodass der gesamte Grafik-Bildschirm 640x480 Pixel groß ist.
Nehmen wir an, du legst dir auf diesem Grafik-SCREEN die x-Achse in der Höhe y-Pixel = 400 horizontal von links nach rechts. Das wäre also relativ weit unten auf dem Bildschirm. Nun legst du weiter drüber einen Graphen, zum Beispiel eine Sinuskurve multipliziert mit irgendeinem Faktor plus eine Konstante, damit sich das alles oberhalb deiner x-Achse im positiven Bereich abspielt. Der Graph wird durch eine Funktion erzeugt. Die y-Werte der Funktion müssen in das Koordinatensystem des Grafik-SCREENs umgerechnet werden.
Die Wertetabelle der Funktion beinhalte zum Beispiel die beiden Werte A = (0 | 100) und B = (1 | 120).
Wo liegt jetzt Punkt A auf dem QBASIC-Grafik-SCREEN? Nicht in Höhe 100. Sondern weil deine x-Achse in der Höhe 400 liegt, müsste der Punkt ja in Höhe 300 abgezeichnet werden. 100 Pixel oberhalb der x-Achse. Wenn du jetzt diesen Wert für das Koordinatensystem - 300 - berechnet hast (aus einem Funktionswert oder einem Messwert aus einer Datei) und du weißt, auf welcher Höhe deine x-Achse liegt. Musst du dann tatsächlich die Pixel dazwischen Pixel für Pixel jeweils +1 abzählen?
Auf der Pixel-Linie zwischen der x-Achse (auf dem Bildschirm in Höhe von 400 Pixeln senkrecht) und dem Graphenpunkt (auf dem Bildschirm in Höhe von 300 Pixeln senkrecht) liegen genau 99 Pixel, wenn du weder das Pixel auf der Achse noch das Pixel auf dem Graphen mitzählst. Das kann man doch als Differenz bestimmen und muss nicht 99 Inkrementierungen machen, um das herauszufinden.
Die kleinste darstellbare Einheit ist auf dem Grafik-SCREEN ein Pixel. Wenn du auf einem senkrechten "Strich" auf dem Bildschirm die Pixel "zählen" willst, musst du deshalb bloß die Koordinaten von "oben" und "unten" miteinander verrechnen, um zu wissen, wie viele Pixel dazwischenliegen.
Ich habe dazu mal eine kleine Grafik erstellt. Die geht aus Gründen der Darstellbarkeit davon aus, dass der Bildschirm nicht 640x480 Pixel habe, sondern bloß 40x30. Durch Anklicken der Grafik gelangt man zur Vergrößerung.
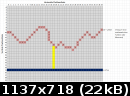
In der Grafik habe ich eine Senkrechte gelb markiert. Musst du die Pixel da tatsächlich einzeln zählen oder gibt es nicht einen geschickteren Weg? Den meint nemored, glaube ich.
Und klar: Zum Beispiel zwischen den X-Werten 0 und 1 liegen überabzählbar viele Zwischenwerte, die zu ebenso vielen Y-Werten führen. Die kann man aber, wenn man mit dem Pixelraster arbeitet, nicht erfassen. Da liegt dann ein bisschen die Parallele zu den Ober- und Untersummen bei der Integral-Annäherung durch die Rechtecke.
Viele Grüße!
Sebastian
_________________

Die gefährlichsten Familienclans | Opas Leistung muss sich wieder lohnen - für 6 bis 10 Generationen! |
|
| Nach oben |
|
 |
nemored

Anmeldungsdatum: 22.02.2007
Beiträge: 4723
Wohnort: ~/
|
 Verfasst am: 17.06.2014, 19:38 Titel: Verfasst am: 17.06.2014, 19:38 Titel: |
 |
|
| Zitat: | Denn ein delta x habe ich nicht vorgegeben. Du nimmst also irgendwo eine Streifenbreite her; d.h. Du integrierst im engen Sinne des Wortes.
Meine Idee war, die Fläche dadurch zu erhalten, dass ich die kleinsten Flächeneinheiten -die Pixel- zähle. Das sind sozusagen die kleinsten Quadrate auf dem Millimeterpapier. |
Selbstverständlich habe ich ein delta x, nämlich den Abstand zwischen den Berechnungspunkten, angegeben durch die Variable schritt, die man selbstverständlich auch anpassen kann, um eine größere Genauigkeit zu erhalten. Wo genau ist der Unterschied, ob ich den Streifen eine fiktive Breite gebe oder du den Pixeln einen fiktiven Flächeninhalt?
_________________
Deine Chance beträgt 1:1000. Also musst du folgendes tun: Vergiss die 1000 und konzentriere dich auf die 1. |
|
| Nach oben |
|
 |
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|



